1. 그래프 (Graph)
정점과 정점 사이를 연결하는 간선으로 이루어진 비선형 자료구조이다
정점과 간선의 집합으로 표현할 수 있다
정점 (vertex)
노드 (node) 라고도 하며 정점에는 데이터가 저장된다
간선 (edge)
링크 (link) 라고도 하며 노드간의 관계를 나타낸다
G(V, E) 로 표현한다
G : graph
V : vertex
E : edge
그 외에 알아둬야할 용어들
Adjacent(인접)
한 정점에서 간선을 한번에 갈 수 있으면 해당 정점들은 인접하다고 할 수 있다
Degree(차수)
한 정점이 가지고 있는 간선(Edge)의 수
진입 차수(In-degree)
방향 그래프에서 외부에서 오는 간선의 수
진출 차수(Out-degree)
방향 그래프에서 외부로 향하는 간선의 수
경로 길이(Path Length)
경로를 구성하는데 사용된 간선의 수
단순 경로(Simple Path)
경로 중에서 반복되는 정점이 없는 경우
사이클(Cycle)
단순 경로의 시작 정점과 종료 정점이 동일한 경우
2. 그래프의 특징
- 정점은 여러 개의 간선을 가질 수 있다
- 크게 방향 그래프와 무방향 그래프로 나눌 수 있다
- 간선은 가중치를 가질 수 있다
- 사이클 (순환경로를 말하며 경로의 시작 정점과 종료 정점이 동일한 경우) 발생 가능
무방향성 (Undirected) : 방향성이 없는 그래프
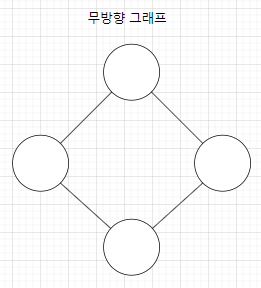
방향성 (Directed) : 방향성이 포함된 그래프

가중치 (Weight) : 간선에 가중치 정보가 포함된 그래프

3. 그래프 구현방법
그래프를 구현하는 방법에는 인접행렬(Adjacency Materix), 인접리스트 방식(Adjacency List)
가 있다 두 개의 구현방식은 각각의 장단점이 있지만 대부분 인접리스트 방식을 많이 사용한다
1) 인접행렬(Adjacency Materix)
- 그래프의 노드를 2차원 배열로 만든것 즉 그래프를 표로 옮겨놓은 것이다
- 각 정점의 연결정보를 0과 1로 표현한다
- 직접 연결된거만 1로 표시하고 간접적으로나 연결이 안된건 0이다
장점
- 2차원 배열안에 모든 정점들의 간선 정보가 포함되므로
배열의 위치를 확인하면 두 정점의 연결 정보를 탐색할 때
O(1)의 상수 시간복잡도가 가능하다
- 구현이 비교적 간단하다
단점
- 모든 정점에 대해 간선 정보를 대입해야 하므로 인접행렬 생성에 O(N^2) 시간복잡도 소요
- 무조건 2차원 배열이 필요하므로 메모리의 낭비가 심하다

2) 인접리스트 방식(Adjacency List)
그래프의 노드들을 연결 리스트로 표현한다
주로 정점의 연결 리스트 배열을 만들어 관계를 설정하여 구현한다
장점
- 정점들의 연결 벙보를 탐색할 때 O(n)의 시간복잡도 (n : 간선의 갯수)
- 필요한 만큼의 공간만 사용하기때문에 공간의 낭비가 적다
단점
- 특정 두 점이 연결되었는지 탐색하려면 인접행렬에 비해 시간이 오래 걸린다
(배열 보다 연결리스트가 탐색속도 느리다)
- 구현이 비교적 어렵다

'CS' 카테고리의 다른 글
| [CS] 힙, 우선순위 큐 (0) | 2022.11.15 |
|---|---|
| [CS] 비선형 자료 구조 (트리) (0) | 2022.11.13 |
| [CS] 스택 (Stack), 큐 (Queue) (0) | 2022.11.12 |
| [CS] 코딩 컨벤션 (0) | 2022.11.10 |
| [CS] 빅오 표기법 (0) | 2022.11.07 |